Im Kapitel "Wie Zahlen klingen" haben wir uns damit beschäftigt, welche Zahlenverhältnisse welchen Intervallen entsprechen und welche Frequenzzahlen eine Partialtonreihe beschreiben.
Wir untersuchten in diesem Kapitel also, wie Intervallstrukturen durch Zahlen beschrieben werden können und welche Zahlenstrukturen "gut klingen".

Im Kapitel "Mit Tönen rechnen" geht es nun darum, wie man mit Zahlen, die Tonstrukturen beschreiben, rechnet.

Bei unserem Vorhaben, mit "Tönen zu rechnen", werden wir zwei Methoden kennen lernen, wobei uns ein bisschen Mathematik wohl nicht erspart bleiben wird:

1. Das Rechnen mit Frequenzzahlen und deren Verhältnissen
2. Das Rechnen mit Centwerten

Rechenaufgabe 1:

Berechnen Sie die Frequenz des zweigestrichenen A (= a''), wenn die Frequenz des eingestrichenen A (= a'), des so genannten Kammer- bzw. Stimmtons, 440 Hz beträgt!

Lösung:

Da das Intervall zwischen a' und a'' eine reine Oktav beträgt und wir aus dem Kapitel "Wie Zahlen klingen" wissen, dass das Frequenzverhältnis für die Oktav  1 : 2  beträgt, müssen wir die Frequenz des a' mit 2 multiplizieren und erhalten für das a'' eine Frequenz von 880 Hz.

Rechenaufgabe 2:

Berechnen Sie die Frequenz des dreigestrichenen A (= a''')!

Lösung:

Wie vorhin multiplizieren wir die Frequenz des a'' mit 2 und erhalten für das a''' eine Frequenz von  880 Hz · 2 = 1760 Hz.

Wenn wir also die Frequenz f₁ eines Tones kennen und ein bestimmtes Intervall nach oben gehen wollen, berechnen wir die Frequenz f₂ des Zieltons durch Multiplikation von f₁ mit jenem Faktor, der dem Frequenzverhältnis des gewählten Intervalls entspricht:

Aus  f₁ : f₂ = a : b  oder besser  f₂ : f₁ = b : a  folgt, dass der passende Faktor  b : a = b/a  sein muss:

Üben wir dies gleich in Rechenaufgabe 3: Berechnen Sie die Frequenzen von e'' und d'!

Lösung:

Zwischen a' und e'' bzw. a' und d' liegt das Intervall einer reinen Quint mit Frequenzverhältnis 2 : 3. Der entsprechende "Umrechnungsfaktor" ist folglich 3/2.

Das e'' liegt eine reine Quint über dem a' und wir erhalten wegen  440 · (3/2) = 660  für das e'' eine Frequenz von 660 Hz.

Der Ton d' liegt hingegen eine reine Quint unter dem a' und wir erhalten mittels Division durch den Faktor 3/2 wegen  440 / (3/2) = 440 · (2/3) = 293,33...  für das d' eine Frequenz von etwa 293 Hz.

Die ganz Fleißigen unter Ihnen können sich nun die Mühe machen und alle Teiltonfrequenzen des großen C nachrechnen und ihre Ergebnisse in der Tabelle "" kontrollieren.

Wem dies aber doch zu mühsam ist, der verwende den eigens dafür entwickelten : Die Eingabe von "66" beim 1. Teilton führt zum gewünschten Ergebnis.

Für Aufgabenstellungen wie oben empfehle ich hingegen schon jetzt einen weiteren elektronischen Helfer: den .

Bevor wir uns jedoch der Centrechnung zuwenden, noch drei Rechnenaufgaben mit Frequenzen!

Rechenaufgabe 4:

Starten wir beispielsweise beim großen C mit 66 Hz!

Anmerkung: Dem findigen Leser wird vielleicht aufgefallen sein, dass ein großes C mit 66 Hz – gleichmäßig temperiert gestimmt – dem a' eine Frequenz von etwa 444 Hz statt 440 Hz aufzwingt. In Wien würden wir das eine "Philharmonische Stimmung" nennen! Bei uns sprechen für diese "hohe Stimmung" jedoch rundungstechnische Gründe.

Gehen wir von diesem großen C mit 66 Hz 12 reine Quinten mit Frequenzverhältnis 2 : 3 aufwärts, so landen wir beim fünfgestrichenen his (= his'''''). Berechnen Sie die Frequenz des Zieltons!

Lösung: 66 Hz · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) · (3/2) = 66 Hz · (3/2)¹² ~ 8563,3 Hz

Rechenaufgabe 5:

Ihr Einwand: Ein his''''' ist doch dasselbe wie ein c''''''!
Mein Einwand: Tja, nur enharmonisch gleich! Berechnen Sie halt die Frequenz des sechsgestrichenen C, das 7 Oktaven über dem großen C liegt!

Ihre Lösung: 66 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 66 · 2⁷ = 8448 Hz

Und Sie sehen: 12 übereinandergeschichtete reine Quinten mit Frequenzverhältnis 2 : 3 sind etwas größer als 7 übereinandergeschichtete reine Oktaven! Und dieser gar nicht so kleine Unterschied hat einen bedeutenden Namen: man nennt ihn das Pythagoräische Komma mit dem Frequenzverhältnis  2⁷ : (3/2)¹² =  2¹⁹ : 3¹² = 524288 : 531441.

Rechenaufgabe 6: Berechnen Sie das Frequenzverhältnis für den temperierten Halbton!

Lösung:

Wir erinnern uns: Ein temperierter Halbton ist der mathematisch exakt 12. Teil einer Oktav.
Um eine reine Oktav aufwärts zu gehen, können wir die Frequenz des Starttons entweder gleich mit 2 multiplizieren oder in Etappen 12 mal den Halbtonfaktor h anwenden:

Wir suchen also jene Zahl "h", die 12 mal mit sich selbst multipliziert – d. h. zur 12. Potenz erhoben – 2 ergibt.
Diese Zahl ist klarerweise die zwölfte Wurzel aus 2.

Das Frequenzverhältnis für den temperierten Halbton lautet somit:

Wie schon im vorherigen Kapitel unter "Die Frequenzen der Teiltöne" besprochen, versteht man unter 1  Cent den hundertsten Teil eines temperierten Halbtons und somit 1/1200 einer reinen Oktav.

Die Maßzahl 100 für den temperierten Halbton legte bereits Johann Gottfried Heinrich BELLERMANN (1832–1903) fest, die Bezeichnung Cent (Abkürzung: C) stammt von Alexander John ELLIS (1814–1890) und bedeutet soviel wie "1% von einem Halbton".

So wie wir bei der Rechenaufgabe 6 das Frequenzverhältnis für den temperierten Halbton ermittelt haben, gehen wir jetzt auch beim Berechnen des Frequenzverhältnisses für ein Cent vor:

Wir suchen nämlich jene Zahl, die 1200 mal mit sich selbst muitipliziert, also zur 1200. Potenz erhoben, 2 ergibt. Dieser "Centfaktor" ist folglich die 1200. Wurzel aus 2 und das Frequenzverhältnis für das Intervall Cent lautet:

Wie man anhand der vielen Nullen nach dem Komma beim "Centfaktor" erkennen kann, ist es eher mühsam mit Frequenzverhältnissen zu hantieren, wenn es sich nicht um einfache natürliche Zahlen handelt. Außerdem entzieht sich ein Frequenzverhältnis als konkrete Größenangabe wohl unserer Vorstellungskraft.

Wir würden viel lieber Intervall-Maßzahlen addieren anstatt Frequenzverhältnisfaktoren zu multiplizieren  –  nach dem Motto:

Und wir sehen: Genau aus diesem Grund wurde das Cent erfunden!

Die einzige Schwierigkeit besteht in der Umrechnung von Frequenzverhältnissen in Centwerte, zumal dabei der Logarithmus dualis, der Logarithmus zur Basis 2, ins Spiel kommt.

Doch keine Angst: alles halb so schlimm!

Wir fragen uns zunächst, was es bedeutet, von einem Startton mit der Frequenz f₁ einen Intervallschritt von der Größe x Cent zu einem Zielton mit der Frequenz f₂ zu gehen. Wie die folgende Gleichung zeigt, müssen wir lediglich f₁ mit dem "Centfaktor" (1200. Wurzel aus 2) hoch x multiplizieren:

Herleitung

Wie in der obigen Formel bereits angeschrieben, brauchen wir aus der Gleichung in der 1. Zeile bloß das x auszurechnen und wir haben eine "Centformel" gefunden, in der uns das x in der Einheit Cent angibt, wie weit zwei Töne mit den Frequenzen f₁ und f₂ voneinander entfernt sind.
Dabei ist die Funktion ld der schon erwähnte Logarithmus dualis, also der Logarithmus zur Basis 2.

Die Herleitung der Centformel wird Sie möglicherweise an Ihre Schulzeit erinnern: Kernstück ist das Logarithmieren der Anfangsgleichung. Da jedoch der mathematische Hintergrund nicht jedermanns Sache ist, habe ich die Herleitung in einem eigenen Fenster verborgen.

In der Praxis ist wohl sogar diese Formel etwas mühsam.
Deshalb steht auf meiner Homepage der schon erwähnte zur Verfügung.

Die Bedienung desselben versteht sich eigentlich von selbst.
Experimentieren Sie nach Herzenslust mit den unterschiedlichsten Intervallen, Centwerten und Frequenzverhältnissen und vergleichen Sie mit der Tabelle ""!

Besonders hinweisen möchte ich auf die Rubrik "Spezielle Intervalle" am .

Sie finden dort unter anderem die wichtigsten Intervalle unseres Tonsystems in der so genannten reinen Stimmung, die eben auf den Intervallen der Teiltonreihe beruht. Auch sind einige für die musikalische Akustik interessante Komata angeführt.

Neben den Intervallnamen sehen Sie in Klammern Kürzel, die Sie anstatt von Frequenzverhältnisfaktoren verwenden können.
Das Kürzel r5 beispielsweise bedeutet rechnerintern nichts anderes als das Frequenzverhältnis der reinen Quint: 3/2.

Zum Abschluss meiner Ausführungen noch etwas für's Auge.

Im folgenden Diagramm sehen Sie die Partialtonreihe und ihre temperierte Näherung in Form von Centwerten bezogen auf den Grundton dargestellt.

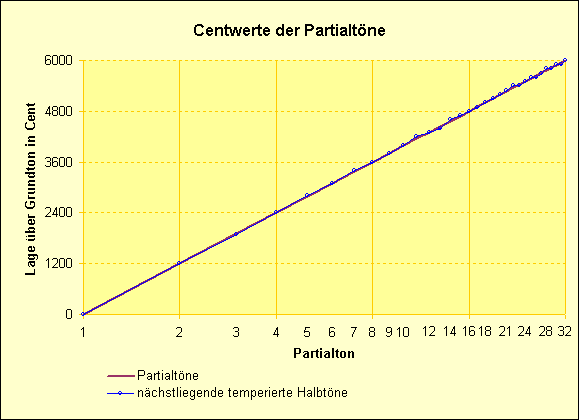
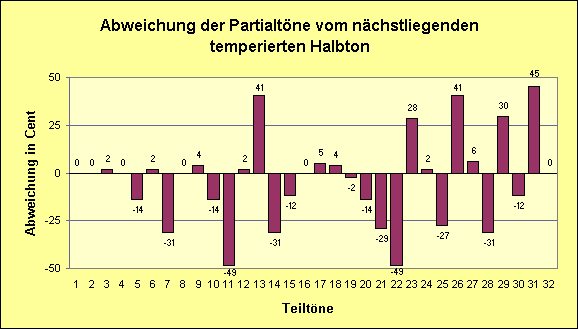
Ein zweites Diagramm zeigt, wie stark die einzelnen Partialtöne von den temperierten Halbtönen unseres Tonsystems abweichen.
Dieses Diagramm dient auch als Demonstration der Einsatzmöglichkeiten und Beweis für die Sinnhaftigkeit der Centrechnung.

Wie Zahlen klingen

Dokumentation