Die Partialtonreihe bis zum 16. Teilton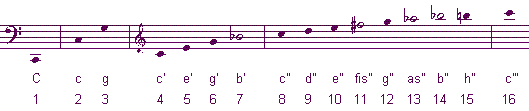
|
|
| partial16.wav Play Stop | klang4.wav klang16.wav |
Die Partialtonreihe vom 16. bis zum 32. Teilton
|
|
| partial32.wav Play Stop | klang32.wav |
Wie Zahlen klingen |
Die Partialtonreihe Die Partialtöne in Noten Die Frequenzen der Teiltöne Töne als Klänge |
Die Pythagoräer – eine vom griechischen Philosophen Pythagoras im antiken Kroton in Unteritalien gegründete religiös-politische Gemeinschaft – glaubten, dass das Wesen aller Dinge in der Zahl bestünde.
Im Bereich der Musiktheorie etwa führten ihre Experimente am Monochord zu einer Intervalllehre, deren Prinzipien noch heute Gültigkeit haben.
Seit den Pythagoräern gelten jene Intervalle als konsonant, also als "wohlklingend", deren Saitenlängenverhältnisse durch einfache natürliche Zahlen ausgedrückt werden.
So stehen beispielsweise bei der reinen Oktav die Saitenlängen der intervallbildenden Töne im Verhältnis 2 : 1.
Heutzutage experimentiert man bekanntlich nicht mehr auf Monochorden, sondern mit Synthesizern und Computern.
In der "Brave New World of Technology" arbeitet man statt mit Saitenlängenverhältnissen mit Frequenzverhältnissen. So betrachtet stehen die Frequenzen zweier eine Oktav entfernte Töne im Verhältnis 1 : 2 – also genau reziprok zum entsprechenden Saitenlängenverhältnis.
Ob antikes Saitenverhältnis oder modernes Frequenzverhältnis, es geht immer um Verhältnisse von Zahlen, die im Reich der Töne zu klingen beginnen.
Im Falle von einfachen Zahlenverhältnissen empfinden wir die entsprechenden Intervalle wie gesagt als konsonant – und eben diese wohlklingenden Intervalle sind es auch, die wir am Anfang der so genannten Partialtonreihe wiederfinden.
Vielleicht haben Sie sich schon einmal gefragt, warum eine Violine anders klingt als ein Klavier oder eine Flöte.
Klarerweise bestehen diese Instrumente aus unterschiedlichen Materialien.
Auch ist die Art der Tonerzeugung jeweils eine andere: Bei einer Geige werden Saiten gestrichen, beim Klavier werden Saiten mit einem Hammer in Schwingung versetzt, und bei der Flöte ist eine schwingende Luftsäule die Ursache, dass die sie umgebenden Luftmoleküle ebenfalls zum Schwingen angeregt werden, Schall sich ausbreitet, auf unser Trommelfell trifft und letztlich im Gehirn das hervorruft, was wir Musik nennen.
Kann man aber dieses offensichtlich unterschiedliche Schwingen einer Violin- und einer Klaviersaite auch physikalisch nachweisen?
Man kann!
Ein von einem Instrument hervorgebrachter Ton ist im Modell nämlich nichts anderes als das gleichzeitige Erklingen von Sinustönen, den so genannten Partial- bzw. Teiltönen des gespielten, natürlichen Tones.
Den ersten, tiefsten Partialton nennt man auch Grundton. Er ist für die Tonhöhe des gespielten Tons verantwortlich.
Alle übrigen Teiltöne heißen Obertöne und bestimmen, je nachdem, wie stark sie beim Klang des gespielten Tons mitmischen, die Klangfarbe desselben.
Die Klangfarbe eines natürlichen Tons wird also vom "Lautstärkenverhältnis" der einzelnen Teiltöne zueinander bestimmt.
All jene Partialtöne, die am Klangaufbau eines natürlichen Tons beteiligt sein können, werden in der so genannten Partialtonreihe oder Teiltonreihe oder Obertonreihe aufgelistet.
Im Anschluss sehen Sie die Partialtonreihe bis zum 32. Teilton des großen C in konventioneller Notenschrift.
Außerdem ist diese Teiltonreihe auch akustisch in Form der Wave-Dateien partial16.wav (1. bis 16. Partialton) und partial32.wav (1. bis 32. Partialton) erfahrbar!
Schließlich runden Überlagerungen der ersten 4 bzw. 16 bzw. 32 Partialtöne in den Hörbeispielen klang4.wav, klang16.wav bzw. klang32.wav einen ersten Ausflug in das Reich der Teiltöne ab.
Die Partialtonreihe bis zum 16. Teilton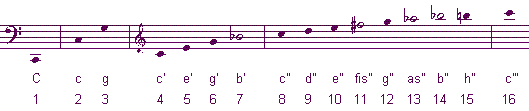
|
|
| partial16.wav Play Stop | klang4.wav klang16.wav |
Die Partialtonreihe vom 16. bis zum 32. Teilton
|
|
| partial32.wav Play Stop | klang32.wav |
In der Tabelle "" sind die Frequenzen der ersten 32 Teiltöne des großen C aufgelistet.
Wie Sie der Tabelle leicht entnehmen können, sind die Frequenzverhältnisse zweier Teiltöne gleich dem Verhältnis ihrer Teiltonnummern (z. B.: 66 Hz : 132 Hz = 1 : 2). Deshalb rechnet man, sofern es um Frequenzverhältnisse geht, am besten gleich mit den Teiltonnummern.
In Folge dessen sieht man auch leicht ein, dass die Frequenzen der Partialtöne allesamt Vielfache des 1. Teiltons, des Grundtons, sind.
In der vierten Spalte der Tabelle finden Sie Hinweise auf für unsere Musik unentbehrliche Intervalle. Angefangen von der reinen Oktav bis hin zur kleinen Terz treten sie zwischen den ersten 6 Partialtönen auf.
Es sind dies also die am Kapitelanfang erwähnten Konsonanzen mit einfachen Zahlenverhältnissen.
Spätestens wenn wir in Spalte 4 auf den großen Ganzton und den kleinen Ganzton zwischen 8. und 9. bzw. 9. und 10. Teilton treffen, wird klar, dass die Partialtonreihe jede Menge weiterer Geheimnisse in sich birgt.
So wird der absolute Abstand zwischen den Partialtönen, von denen es rein theoretisch unendlich viele gibt, immer kleiner.
Diese Tatsache ist der Spalte 4 zu entnehmen, wobei das hier verwendete Größenmaß Cent nicht jedermann und jeder Frau geläufig ist: 1 Cent entspricht genau 1/100 Halbton. 100 Cent ergeben somit einen temperierten Halbton, und da eine Oktave aus 12 Halbtönen besteht, misst eine reine Oktav 1200 Cent.
(Für weitere Informationen zum Cent-Maß verweise ich auf das Kapitel "Mit Tönen rechnen".)
Und da sind wir bereits beim nächsten Problem: Den so genannten temperierten Halbton mit einer Größe von 100 Cent, der mathematisch exakt der 12. Teil einer Oktav ist und die Grundlage der heute üblichen gleichmäßig temperierten Stimmung unseres Tonsystems darstellt, diesen temperierten Halbton werden Sie in der gesamten Partialtonreihe nicht finden!
Dies ist auch der Grund, weshalb alle Partialtöne – mit Ausnahme des Grundtons und seinen Oktavverwandten – mit keinem Ton unseres gleichmäßig temperiert gestimmten Tonsystems identisch sind!
Um das zu demonstieren habe ich in der letzten Spalte der Tabelle "" angegeben, wie weit die einzelnen Partialtöne vom nächstgelegenen temperierten Halbton entfernt sind.
Die mehr als 15 Cent entfernten Teiltöne sind im obigen Notenbeispiel ("Die Partialtöne in Noten") mit hohlen Köpfen dargestellt.
Im folgenden Diagramm kann man nicht nur in trockenen Zahlen, sondern auch optisch verfolgen, wie stark die auf einer exponetiell ansteigenden Kurve gelegenen Frequenzen der Partialtöne von jenen der naheliegensten temperierten Halbtöne abweichen.
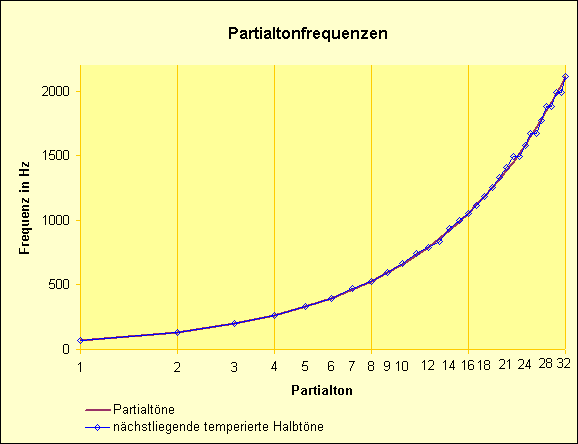
Besonders deutlich wird dies in einem vergrößerten Ausschnitt der 5. und 6. Partialtonreihenoktav:
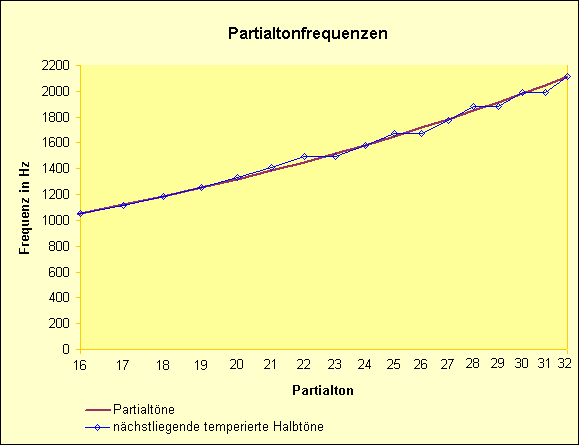
Zum Abschluss dieses Kapitels noch ein paar Worte zum Begriff "Ton".
Unter Ton verstehen nämlich Musiker und Physiker nicht immer dasselbe!
Für den Physiker ist ein Ton zumeist ein "reiner" Sinuston, der von sinusförmig schwingenden Molekülen hervorgerufen wird. In der folgenden Abbildung kann man die Sinuskurve der Grundschwingung und der drei Oberschwingungen leicht erkennen.
Wie im Unterkapitel "Die Partialtonreihe" ausgeführt, entsteht ein auf einem Instrument gespielter oder ein gesungener "natürlicher" Ton durch das gleichzeitige Erklingen mehrerer Sinustöne, den Partialtönen – also durch eine Überlagerung von Sinusschwingungen.
Ein durch Überlagerung von Sinustönen entstandener Ton ist für den Musiker halt einfach ein Ton, für den Physiker hingegen ein Klang.
In der Abbildung oben ist ein – der Übersichtlichkeit halber – von nur vier Partialtönen gebildeter Klang modellhaft dargestellt. Da die Amplituden der vier Teiltöne gleich groß sind, ist ihr Lautstärkenanteil am Gesamtklang gleich stark.
Mit der Wave-Datei klang4.wav können Sie diese Abbildung zum Klingen bringen: Sie hören zunächst den Grundton mit 66 Hz; jede Sekunde tritt dann ein weiterer Oberton zum Klanggeschehen hinzu.
Die Beispiele klang16.wav und klang32.wav bauen nach dem selben Prinzip Töne mit 16 bzw. 32 gleich intensiven Partialtönen auf.
|
|
Mit Tönen rechnen
|